Pentagonal Numbers

I belong to the group of scientists who do not subscribe to a conventional religion but nevertheless deny that the universe is a purpose less accident. The physical universe is put together with an ingenuity so astonishing that I cannot accept it merely as a brute fact. There must be a deep level of explanation.

- Paul Davies, The Mind of God

Number systems are built according to different rhythms.

-Annemarie Schimmel, The Mystery of Numbers

A quick search (I don't prefer the new term, "googled it" ! ) on Pentagonal Numbers, yields wonderful images of Pythagorean appetite of this construction. Not many know Pythagoras is beyond the "Right Angled Triangle"! He was a Philospher, Theologian and Mathematician. The clan who learned under him were called Pythagoreans and did not divulge their knowledge so easily for reasons then known to be divine. Sadly they were massacred. Anyway, this posting is about Pentagonal Numbers.

What are Pentagonal Numbers can be learnt from the references(for Mathematicians and Non-mathematicians) below. What I learned from the history is what the post is about. A very beautiful and important theorem involving pentagonal numbers was discovered by 18th century mathematician Leonhard Euler. One day he started to multiply out the infinte product, a mathematical sequence, and found that the first few terms' exponents were pentagonal.

Infinite Product - (1-x)(1-x^2)(1-x^3)(1-x^4)…
The first few terms - 1-x-x^2+x^5+x^7-x^12-x^15…
One can test this with the below formula for positive and negative values of n and arranging the resulting nubers in ascending order.

½ n(3n-1)

Based on the formula we get the dots for the nth pentagonal numbers.
The pentagonal formula generates 1,5,12,22,35... that is,
For n=1, we get a value 1.
For n=2, we get a value 5.
For n=3, we get a value 12.

where A=1, B=5, C=12, D=22, E=35


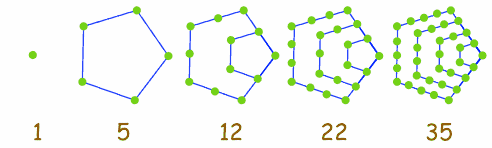
What is weird is the formula also produces values for n when it is negative. Here it is
Negative n - ... 40 26 15 7 2 0
Positive n - 0 1 5 12 22 35 51...

If we put it in a Que it would be as follows

... 40 26 15 7 2 0 1 5 12 22 35 51...

Let us arrange the above numbers in ascending order.

1 2 5 7 12 15 22 26 35 40 51 57 ...

Take successive differences and we get:
1 2 5 7 12 15 22 26 35 40 51 57 ... ~~~~~~ the series
1 3 2 5 3 7 4 9 5 ~~~~~~~~~~~~~~ the differences

Now I have skipped alternate differences and what we get is 2 sets:

• A set consisting of natural numbers; marked bold
• A set consisting of odd numbers; not marked bold

Isn't it spooky!!!

Do all numbers belong to more than one class of polygonal numbers? it turns out that there is a simple test for determining whether a number is a polygonal number for an n-sided polygon. Here is a secret recipe.

• Pick a number.
• Multiply it by 8(n-2) and add (n-4)2 to the product. If the result is a square, then the number is a polygonal number for n-sided polygon.
  

References

• http://en.wikipedia.org/wiki/Pentagonal_number
• http://mathworld.wolfram.com/PentagonalNumber.html
• As usual my own efforts of reading :-)
• ^ means raise to; x^ 2 means "x raise to 2"